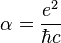|
| Ernst Stückelberg |
Some of these equations can only be described as breath taking. The most famous is probably E=mc2. The equation linking energy and mass. Another is Newton's F=ma. Planck's E=hf is a third.
Simple equations that give us insight into the way the universe behaves. Yet there are other parts of physics where the mathematics is exceptionally difficult.
Take the Einstein field equations, still can't figure most of this out. Well hard. Most of quantum mechanics, or take the strong nuclear force, before you know it your staring down at something like this bad boy
it is at this point that most of us reach for our coats and head off home. This is just the way of it sometimes. There are lots of areas in physics were the best models are still mind numbing for the majority of people. These are the best solutions we have found so far. For me this raises two questions. Are there actually better theories out there that are more simplistic that we haven't found yet? Or is mathematics alone not the best method of describing everything in Physics?
The greatest step forward in "alternative" methods of describing the physical universe are probably the Feynman diagrams (first thought up by Ernst Stückelberg apparently, who was also the first to propose that a positron may be an electron travelling backwards in time).
Richard Feynman used the diagrams back in 1948 as a pictorial representation of events.
Take something "simple", an electron and a positron meeting each other, annhiliating each other to create a photon that then converts back to a positron and an electron. The maths for this is based on something called a Scattering-matrix that looks something like this
Let's be honest it takes you half an hour just to try and say it out loud. Then half a day trying to figure out what each of the terms in the equation actually represents.
The Feynman diagram on the other hand looks like the diagram below left. You can see the positron and electron meet, create a photon that then turns back into a positron and an electron.
 |
| Electron - Positron interaction |
They are so handy that there will be a future post completely dedicated to the use of Feynman diagrams and the rules governing their use. There you will find out how to describe some of the most complex physics ideas without the use of a single equation. Which brings me back to the point of this post.
Physics will always rely on mathematics to a large degree. The 20th century advancement in physics as been driven by mathematics. I wonder though, if we will reach a point where maths can take us no further and in order to open up the next great epoch in physics advancement will require a new set of tools based on something we can't even imagine just yet. Best get my thinking cap on.
I can feel a great idea coming on, where are those crayons?