|
| Something from nothing? |
This post is my musings on the conservation of energy.
Before we get started, I have posted previously on the idea that I think that the angular and linear momentum of the universe is actually zero. I have no proof of this and there is currently no accepted answer to the question. In fact it is actually very difficult to even ask the question, because we end up having to make a lot of assumptions or guesses. Firstly, we don't know that the big bang theory is correct. Yet this will definitely have an impact on any answer we try to derive.
Conservation of energy works on all the tests we have done on a small scale, so I am going to assume that the universe is a good sport and is happy to play by the rules. So, total conservation of momentum, angular and linear, is zero. I go further to suggest that the total electric charge of the universe is also zero.
Finally to the subject of this post. I think that the total energy of the entire universe is zero. Or, if not zero, some fixed value. This is a bit of a wild idea, no doubt about it. We have back ground radiation, we have planets and suns all with mass, which according to Einstein is just energy sort of condensed. If you add up all the electro magnetic radiation in the universe and add up all the mass of all the planets and stars you most certainly do not get zero. So, just what am I going on about. Well ..
The net energy in the universe is zero or a constant value. All the energy we see is offset by a SpaceTime energy field. I don't think that it makes sense for SpaceTime to just be some frame of reference.
Time is real. I may not understand time, I know that there is a past I can remember it. I know that there is a future and I will die at some point in that future. This is an absolute fact. While I may not know the hour of the event, I am 100% certain that it will come to pass. Therefore the future which contains set results exists. There is more on this idea in another post. But for today I will content myself with the idea that SpaceTime is not an abstract idea but something that is an integral part of the real universe.
So say SpaceTime is actually the equivalent of negative energy and negative mass. We believe that the universe it about 13 billion years old and continues to get older a day at a time. So if this means that we're making more SpaceTime each and every second of each and every day and if this is the case then this must be balanced by real matter and energy. I think that this is the case.
If this was so, we would expect to see the conservation of energy/mass violated at some point as the new mass and energy suddenly pops into existence. This has not been seen yet. So it is either wrong, or we have not seen the conditions under which this may actually happen.
I think that the conditions for energy/matter to "spontaneously" occur are low vacuum and low gravitational field. The only places we see this are deep space. Further, I have a feeling that the particles that appear as if by magic are probably neutrons. Which decay pretty sharpishly into protons, electrons and an anti electron neutrinos.
Can I prove any of this? not at the moment no, but I am working on it.
Time is real. I may not understand time, I know that there is a past I can remember it. I know that there is a future and I will die at some point in that future. This is an absolute fact. While I may not know the hour of the event, I am 100% certain that it will come to pass. Therefore the future which contains set results exists. There is more on this idea in another post. But for today I will content myself with the idea that SpaceTime is not an abstract idea but something that is an integral part of the real universe.
So say SpaceTime is actually the equivalent of negative energy and negative mass. We believe that the universe it about 13 billion years old and continues to get older a day at a time. So if this means that we're making more SpaceTime each and every second of each and every day and if this is the case then this must be balanced by real matter and energy. I think that this is the case.
If this was so, we would expect to see the conservation of energy/mass violated at some point as the new mass and energy suddenly pops into existence. This has not been seen yet. So it is either wrong, or we have not seen the conditions under which this may actually happen.
I think that the conditions for energy/matter to "spontaneously" occur are low vacuum and low gravitational field. The only places we see this are deep space. Further, I have a feeling that the particles that appear as if by magic are probably neutrons. Which decay pretty sharpishly into protons, electrons and an anti electron neutrinos.
Can I prove any of this? not at the moment no, but I am working on it.




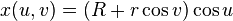

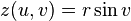

 , where
, where