For those unaccustomed to these little fellas, these numbers are the result of taking the square root of a negative number. For example, the square root of -4 is not -2. After all
(-2) x (-2) = 4
the square root of -4 is 2i so
(2i) x (2i) = 4i2 = 4 x (-1) = -4, because i x i = i2 = -1
so any number that is the square root of a negative number is called... imaginary. We say that they do not exist, so they are imaginary. A trick of mathematics, if you will. This, for me, is where we are going wrong.
There is nothing imaginary about these number they are just a different branch of mathematics and for physics they are invaluable. Without them it is impossible to describe photons mathematically. Electric and magnetic fields just don't work. Quantum mechanics would probably not exist at all.
Yet I find that when we talk about the "imaginary" component of a vector or field or whatever something in my brain discounts it almost. It is as if my brain is saying , yep, it allows us to describe something mathematically, but it does not exist in the real world. A bit like saying that atoms are not real but just mathematical abstractions, which is complete nonsense.
The universe is built on imaginary numbers, so they cannot be imaginary, I can see them at work every time I look at the sun or the moon or pretty much anything. You try describing anything and sooner or later the imaginary number will raise its head. Not only that but it also pops up in one of the most, if not the most amazing of equations.
Now, it has been noted that I do go in for a bit of mathematician bashing, but on this occasion I salute them, get a load of this
This is known as Euler's identity or Euler's equation. This equation has addition, multiplication and an exponential. It contains five fundamental mathematical constants:
- The number 0, the additive identity.
- The number 1, the multiplicative identity.
- The number π, (π = 3.14159265...)
- The number e, the base of natural logarithms, which occurs widely in mathematical and scientific analysis (e = 2.718281828...). Both π and e are transcendental numbers.
- The number i, the imaginary unit.
Some consider it to be one of the most beautiful equations of all and I find myself agreeing with them. It says so much in such a small equation, a little like E=mc2.
Also,
eiπ = cos π + i sin π which is just a specific solution of
eiωt = cos ωt + i sin ωt
which is the starting point of describing how a photon travels through space.
So, imaginary numbers give us beautiful equations and help us to explain the universe... Can this be right? maybe I am imagining it after all.
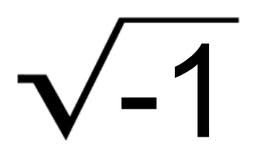




No comments:
Post a Comment